最近一直都在瞎忙，一想到10月中旬Omont要来了，就觉得十分紧张，要看的东西太多太多了，而后果就是实际上看得很少，这是拖延症的典型吧。今天整理邮件的时候突然翻到了以前写的东西，觉得贴在博客上充数还是可以的。于是，就贴个了帖子。因为本人不懂宇宙学，所以文字里面很多漏洞啊啥的……欢迎过客们留个脚印哈～

引子

宇宙学近来一直是天文研究的热门主题。尽管现在早已是一个精确宇宙学的时代，但人们对于宇宙的认识仍不够深刻。平坦的宇宙模型普遍被认为目前最合理的宇宙模型，即我们的宇宙是平坦的，且主要由冷暗物质和暗能量构成，这些成分决定了宇宙的时空几何性质。但这个模型是否能很好的和观测事实相符，或者说我们观测到的宇宙是否真的是由75%左右的暗能量以及25%左右的物质(包括重子物质和暗物质)构成，这还需要我们做进一步的验证。而在这个验证过程中，有一个参数起到重要的作用，即哈勃常数。
根据哈勃关系，我们知道，即通过准确测量天体到观测者的距离及其红移值，(在近邻宇宙）我们就可以得到哈勃常数。目前有多种测量天体距离的方法。例如有通过测量天体的光度距离来计算哈勃常数的方法，但测量光度距离时存在着消光改正的问题;另外如果光度距离的估计对象是造父变星，观测者则还需考虑造父变星的金属丰度对周光关系的影响，即其周光关系需要精确的定标，才能很好的应用到河外星系的造父变星当中，进一步推算出星系的距离；除此之外，不少人通过对于Ia型超星新的数据研究发现，Ia型超星新作为标准烛光存在着一些问题（文献自己找吧）。人们对于这些数据仍存有一些争议。于是，利用独立于光度距离方法之外的方法直接测量哈勃常数就变得非常重要。在1999年Herrnstrin等人分别利用VLBI和单天线对NGC 4258进行了长时间的详尽观测(Herrnstein et al. 1999)，并结合动力学的方法直接而准确的得到了NGC4 258的距离。尽管该星系按照宇宙学尺度来看离我们较近，但是如果能够寻找到更远的类似于NGC 4258的天体，将会给我们直接测量哈勃常数提供一个十分可观的方法。即如果能在哈勃流中找到类似NGC 4258这样的星系（具有盘状结构分布的巨水脉泽）。我们将大大提高哈勃常数的测量精度，从而更加有效的限制我们现有的宇宙学模型中的各种参数，帮助我们更加深入的了解暗能量的本质。所以说，利用河外星系中的巨水脉泽来测量哈勃常数是一个十分有意义的测量方法，值得我们深入的探讨和研究。

哈勃常数和宇宙学模型

自从哈勃在1929年发现了哈勃定律(Hubble 1929)之后，宇宙学开始有了很大的发展。哈勃利用造父变星的周光关系得到了24个星系中的造父变星的光度，再用距离模数求出他们的距离，同时测量他们的光谱中谱线的红移，得到红移值。最后得到了著名的哈勃定律。图1 (Freedman & Madore 2010)就是哈勃在1929年测量的24个星系的退行速度-距离图。

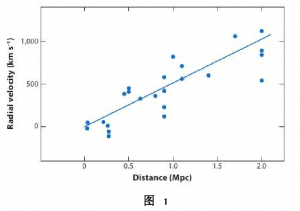
可以看到这些点基本符合一个线性的关系，即距离越远，退行速度越快(，然而由于当时哈勃没有意识到造父变星周光关系受星族的影响，星族I和星族II的周光关系并不相同，也就是说具有不同金属丰富的造父变星其周光关系不同。因此，当年哈勃测量的哈勃常数并不准确。根据现有的宇宙学模型，宇宙由重子物质 (Baryons)、冷暗物质(Cold Dark Matter)和暗能量()构成，这三者一起决定了我们宇宙的几何物理性质。下面的式子表达了这几个宇宙学参数和哈勃常数的关系，

(1)  

其中是红移，表示红移为处的哈勃常数，表示红移为处的哈勃常数，表示物质密度，表示暗能量的密度，而是暗能量的状态方程，即压力和能量密度之比。前一项主要起到的作用是让宇宙收缩，而后一项是让宇宙膨胀。
根据Freedman方程，我们知道压力和能量一起决定了宇宙的膨胀性质，即

(2)  

式中a是尺度因子，G是引力常数，k是宇宙的曲率。我们可以看到密度和压力P一起决定了宇宙的膨胀性质。根据我们目前观测的结果，宇宙处于加速膨胀的阶段，也就是说，如果压力是负值，那么我们可以比较容易的解释观测的结果。而现在观测的结果表明，如果我们引入宇宙学常数，我们则需要让，用来解释宇宙现有的加速膨胀。另外，人们也根据WMAP对CMBR的观测分析其涨落来研究暗能量。有人提出，如果能在小于3%的误差范围内精确测定哈勃常数，那么将是对CMBR数据的有力补充，会更有效的限制暗能量的模型（Hu et al. 2005）。

无论如何，哈勃常数的精确测定对我们了解宇宙，探究暗能量本质，并得到宇宙学中一些重要的参数都有至关重要的意义。如果要解释宇宙现有的加速膨胀的物理状态，我们需要精确测量出哈勃常数。同时，在河外天体的观测中，哈勃常数也有重要的意义，通过天体红移值正确估计哈勃流中的天体到观测者的距离需要精确的哈勃常数，当然也同时需要我们更加准确的估计出星际消光的作用大小。目前，根据Freedman等人给出的结果：哈勃常数值应该为，其中第二项为随机误差，第三项为系统误差(Freedman&Madore 2010)。

哈勃常数测量与河外巨水脉泽

距离的测定在天文学中是一个比较困难的间题。目前人们主要依靠造父变星的周光关系，红巨星分支的顶点，漩涡星系的Tully-Fisher关系，星系的表面亮度波动以及I。型超新星等方法来测量距离。这些距离有的是光度距离有的是角直径距离。对于光度距离而言，例如造父变星的周光关系，是目前主流的测量方法。哈勃太空望远镜(HST)的关键项目(Freedman et al. 2001)就是利用大麦哲伦云(LMC)中造父变星对周光关系定标，并应用到其它河外星系，计算出他们的距离，从而测出哈勃常数。然而如果只用LMC定标，用这个方法得到的哈勃常数仍然会存在10%的误差。另外，金属丰度对周光关系也存在影响，用不同的金属丰度会得到不同的哈勃常数(Sandage et al. 2006);尽管Tully-Fisher关系是现在应用的最广的测距方法，他却有15%-20%的误差(Tully& Pierce 2000)。而河外巨脉泽方法不同于测量光度距离，这种方法测量的是天体的角直径距离。他独立于光度距离测量法。
第一个河外巨水脉泽由Churchwell于1977年发现，它位于M33中，光度达到，其光度是银河系内普通脉泽源的200倍。河外巨脉泽源往往与星系核活动密切相关。他们主要分为两类，第一类和活动星系吸积盘成协，比如NGC 4258;还有一类是由星系核的射电喷流与周围分子云相互作用引起的，如NGC 1052。目前观测到的具有水脉泽的河外星系共有100多个，其中只有三分之一是属于第一类的巨水脉泽(Braatz et al. 2007)。

在1999年，Herrnstein等人对Seyfert2型星系NGC 4258(侧向)做了详细的观测，发现NGC 4258有巨水脉泽，并且其运动可以很好的用开普勒定律来解释。从而通过简单的动力学知识，假设这些脉泽是在围绕着星系中心黑洞运动的翘曲的盘上，就可以准确测出这个星系的距离。Herrnstein等人使用VLBA对该星系做了成图观测（如图2，Herrnstein et al. 1999），用来测量星系中脉泽源分布的几何结构。他们从观测推测出巨水脉泽是分布在一个侧对这观测者的薄盘上，这个盘主要由气体构成，从距离中心黑洞～0.14-0.28pc处开始出现。同时，他们用单天线观测其22GHz附近的谱线和和其移动。推算出盘围绕星系中心做开普勒运动，绘制旋转曲线，并求解出中心天体的质量为，因此推断NGC 4258中心确实存在黑洞。通过测量巨脉泽运动的速度和加速度我们就可以得到这个星系距离的距离，因为有如下关系(Herrnstein et al. 1999)：

(3)  

和

(4)  

式中表示以Mpc为单位的巨脉泽距离；表示在处的方位角；等于，这个量可以从旋转曲线估计出来；代表了盘的角速度投影，这个量可以从速度-位置图中测出，即为速度-位置梯度。根据上面的两个式子，测量脉泽的自行或者加速度这两个方法都分别可以得到NGC 4258的几何距离。
由于NGC 4258离我们的距离约为7.2Mpc (Herrnstein et al. 1999)，因此其自身的运动速度可能会混淆哈勃流的速度，所以我们不能用NGC 4258准确测量哈勃常数。而需要更加遥远的巨脉泽源，同时我们需要像GBT或者是Effelsberg这样灵敏度更高的望远镜去发现和监测巨脉泽的谱线，这两个设备可以探测到距离我们大约50-200Mpc范围内的星系，这些星系处于哈勃流中，可以用来限定哈勃常数。我们还需要使用VLBI对这些源成图观测，得到其几何结构(角直径)。通过估计，加上盘模型本身的误差，可以估计出利用巨脉泽测量哈勃常数的误差大约为5%，而星系和星系之间并没有统计上的相关性，所以误差和星系数量的1/2次方成反比。所以我们可以提高观测星系的数量，从而减小误差，使其降低到~3%以下。
尽管现在观测到大约30多个具有盘状结构巨水脉泽源，但目前其中只有2个星系有很好的观测结果。NRAO和其它几个天文研究机构成立了一个河外巨脉泽项目(Magemaser Cosmology Project, MCP)小组，旨在通过此种办法精确的测量哈勃常数。到目前位置他们发现了UGC 3789和NGC 6323这两个类似于NGC 4258的理想源，MCP小组深入观测了这两个源，得到了哈勃常数，同时也给造父变星提供了很好的定标。图3给出从1977年到2009年间发现的河外水脉泽源数量的统计情况(Braatz et al. 2010)。随着观测设备技术的提高，越来越多的河外水脉泽源被发现，其中GBT起了不可估量的作用。

MCP小组采用的测距方法基于Herrnstein的方法，考虑一个侧向的开普勒盘运动模型，直接得到河外星系的角直径距离。首先设想一个侧向我们的平坦薄盘，而盘的运动由中心的黑洞主导，水脉泽沿着圆轨道分布在其周围的分子云中。在这个模型中，这些脉泽分布在位于围绕中心天体旋转的盘上，一起做开普勒运动。因此，如果把脉泽源的速度和位置联合起来做图，那么我们会看到这些源将分布在几条线上。我们在盘上选取任意两个点和，那么可以得到其平均速度以及角大小。那么就有，

(5)  

式中a为向心加速度，r为选取的脉泽源之间的空间距离，为其对应的角直径。在实际观测中，通常不会直接测量角直径和速度，而是测量开普勒常数k和曲率常数。一方面根据拟合旋转曲线，得到常数k；另一方面通过测量速度-位置图的倾斜来得到曲率常数。最后可以将星系的距离表达为，

(6)  

对应的相对误差为，

(7)  

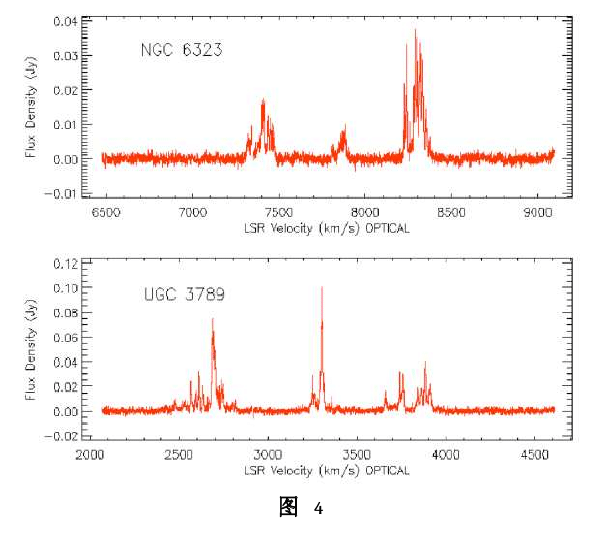
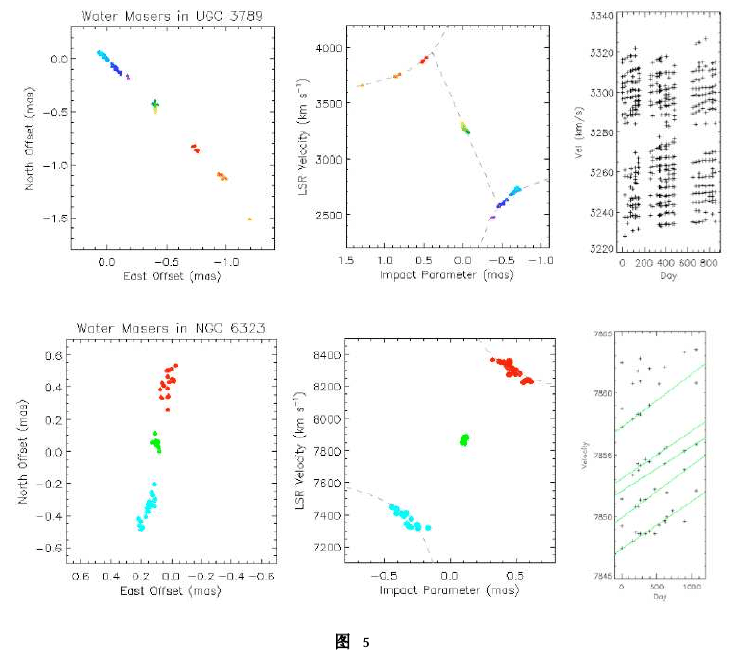
即只需测量其向心加速度a，开普勒常数k以及曲率常数就可以测出其几何距离，测量结果的相对误差决定于这三个测量值的相对误差。MCP小组利用GBT单天线望远镜拍摄了这两个星系的巨水脉泽谱线，图4所示(Braatz et al. 2010)，然后他们用VLBI分别观测UGC 3789和NGC 6323，得到他们的速度一位置曲线和自行。图5所示(Braatz et al. 2010）。根据UGC 3789给出的测量结果，算出的退行速度是~，距离是51 Mpc，这说明UGC 3789处在哈勃流中，求出的哈勃常数约为 (Braatz et al. 2010)。而NGC 6323的观测结果并不是令人十分满意，现在只能了解到，其距离大约为100 Mpc。这个距离很远，所以我们需要更为精准的测量才能很好的确定出哈勃常数，这就要求我们提高仪器的分辨率和灵敏度。

河外巨水脉泽测量哈勃常数的局限性

从前面的介绍中我们看到了利用河外星系巨水脉泽测量距离的巨大潜力，但同时这种方法也受限与很多方面。首先我们需要对河外星系中的脉泽源做成图观测。根据经验，河外星系的脉泽源分布的尺度大约在0.1pc的尺度范围上，如果想在这个精度下做观测，望远镜的分辨率至少要在亚毫角秒的量级，甚至更小。NGC 6323的观测已经达到了VLBI的分辨率极限，所以，如果要想更有效的使用这个方法测量哈勃常数，我们必需要提高现有仪器的分辨率。另外，我们还要同时监测这些脉泽的谱线，这对现有设备的灵敏度也提出了挑战。所以这个方法虽然没有消光、金属丰富等等因素的影响，但对于现有设备的要求比较高，所以现有探测到的星系数量还不足以提供有效的哈勃常数限制。无论如何，这三个星系的结果可以作为很好的定标源，用来校准造父变星的周光关系，间接的对限制哈勃常数做出了贡献。

参考文献

• Herrnstein, J et al, 1999, Nature, 400, 539,
• Freedman, W. L. and Madore B. F, 2010, ARAA, 48, 710,
• Hu, W., 2005, ASPC, 339, 215,
• Freedman, W. L. et al，2001, ApJ, 533, 47,
• Sandage, A. et al, 2006, ApJ, 653, 843,
• Tully, R. B. and Pierce. M. J., 2000, ApJ, 533, 744,
• Reid, M. J. et al，2009, ApJ, 695, 287,
• Braatz, J. A，2010, ApJ, 718, 657,
• Hubble, E. P，1929, ApJ, 69, 103.

p.s. 这其实是“观测宇宙学”的作业，哈哈。