A few days ago, I was trying to do the convolution between a Sinc function and a Gaussian function. But I got stuck from the first step, when I tried to solve that by using the convolution theorem, namely the Fourier transform of the Sinc(x), although I knew it is very easy to find the right answer by Googling or Mathematica. But it is worth a try to be done by hand. So, here we go:
We know that the Fourier transform of Sinc(z) is,
![\[\int_{-\infty}^{+\infty} {{\sin(z)}\over{z}} e^{-i \omega z} dz\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-9857c71e7449738adac353cacb249874_l3.png "Rendered by QuickLaTeX.com")
and
![\[\int_{-\infty}^{+\infty} {{\sin(z)}\over{z}} e^{-i \omega z} dz = \int_{-\infty}^{+\infty} {{e^{iz}-e^{-iz}}\over{2iz}} e^{-i \omega z} dz.\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-3ae26f5ec9c4af02ce39e689a864f724_l3.png "Rendered by QuickLaTeX.com")
(1) 
Let us consider the first item, when 
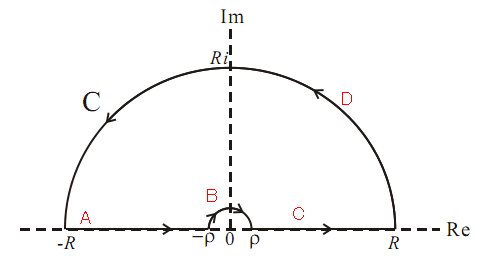
, namely 
, we can choose the path below to do the contour integration.
Using the method of complex residues, we take the contour with no singular point, separating the path into four parts, namely A, B, C and D shown as the red letters in the figure. Thus,
(2) 
Also if , namely 
, and when 
and 
, it is easy to prove using Jordan’s lemma, that the fourth term is equal to zero. Thus we can the rewrite the rest items as,
![\[\int_{-\infty}^{0_{-}}{{e^{i(1-\omega)z}}\over{z}} dz+\int^{+\infty}_{0_{+}}{{e^{i(1-\omega)z}}\over{z}} dz =\int_{-\infty}^{+\infty}{{e^{i(1-\omega)z}}\over{z}} dz =-\lim_{\rho \to 0} \int_{B}{{e^{i(1-\omega)z}}\over{z}} dz.\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-8d151157ec44311f23d156f6477cd4f9_l3.png "Rendered by QuickLaTeX.com")
In order to calculate the value of the item on the right side, I use 
, so 
, then we have,
![\[\lim_{\rho \to 0} \int_{B}{{e^{i(1-\omega)z}}\over{z}} dz=\lim_{\rho \to 0}\int_{\pi}^0 \exp[i (1-\omega) \rho e^{i \theta}] i d\theta=\int_{\pi}^0id\theta=i(0-\pi)=-i \pi.\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-29c327f9704a979e61027493124322ec_l3.png "Rendered by QuickLaTeX.com")
So, in the end, we get the value of the first integration item shown in the Eq.(1),
(3) 
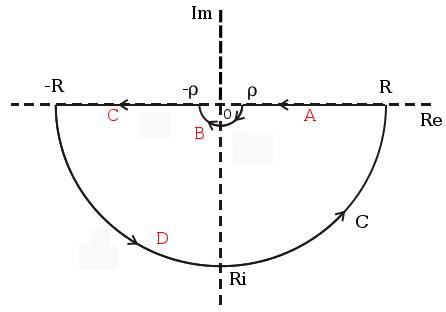
When 
, according to Jordan’s lemma, we can not get the fourth item in the Eq.(2) to be zero. So we have to choose another path for finalizing the integration.
So I chose the path below to deal with such a situation,
It is not hard to calculate the same way as the previous one,
(4) 
and here again I use the same trick, 
, so 
. Because ,
![\[\lim_{R \to \infty} \int_{B}{{e^{i(1-\omega)z}}\over{z}} dz=\lim_{R \to \infty}\int_{\pi}^0 \exp[i (1-\omega) R e^{i \theta}] i d\theta=\int_{\pi}^0 0 \times id\theta=0,\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-ee14e2cee67b9cbbdb379e4d63fef4cc_l3.png "Rendered by QuickLaTeX.com")
![\[\lim_{\rho \to 0} \int_{B}{{e^{i(1-\omega)z}}\over{z}} dz=\lim_{\rho \to 0}\int^{\pi}_0 \exp[i (1-\omega) \rho e^{i \theta}] i d\theta=\int^{\pi}_0 i d\theta=i(\pi-0)=i \pi.\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-63b97ad45dad96e3947acb2eff4774db_l3.png "Rendered by QuickLaTeX.com")
(5) 
Now, let’s move on to the second part in the Eq.(1). Following the same steps, using contour above real axis I get,
(6) ![\begin{equation*} \int_{+\infty}^{-\infty}{{e^{-i(1+\omega)z}}\over{z}} dz = \lim_{\rho \to 0}\int_{\pi}^0 \exp[-i (1+\omega) \rho e^{i \theta}] i d\theta = -i\pi,\quad \omega< -1; \end{equation*}](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-0b488fc6dd93f424add8a7f379418556_l3.png "Rendered by QuickLaTeX.com")
and using contour blow real axis I get,
(7) ![\begin{equation*} \int_{+\infty}^{-\infty}{{e^{-i(1+\omega)z}}\over{z}} dz = \lim_{\rho \to 0}\int^{\pi}_0 \exp[-i(1+\omega) \rho e^{i \theta}] i d\theta = i\pi,\quad \omega>-1. \end{equation*}](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-63081702195c44f750655d7a08fc49e0_l3.png "Rendered by QuickLaTeX.com")
Finally, we can write the answer as, if 
![\[\int_{-\infty}^{+\infty} {{\sin(z)}\over{z}} e^{-i \omega z} dz={1 \over {2i}} \int_{-\infty}^{+\infty} {{e^{i(1-\omega)z}}\over{z}} dz + {1 \over {2i}} \int_{+\infty}^{-\infty} {{e^{-i(1+\omega)z}}\over{z}} dz={{\pi}\over2}+{{\pi}\over2}=\pi;\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-b654a4b1f1df6d655afc364b160b153e_l3.png "Rendered by QuickLaTeX.com")
and if and 
![\[ \int_{-\infty}^{+\infty} {{\sin(z)}\over{z}} e^{-i \omega z} dz={1 \over {2i}} \int_{-\infty}^{+\infty} {{e^{i(1-\omega)z}}\over{z}} dz + {1 \over {2i}} \int_{+\infty}^{-\infty} {{e^{-i(1+\omega)z}}\over{z}} dz={{\pi}\over2}-{{\pi}\over2}=0.\]](https://eagle.lamost.org/wp-content/ql-cache/quicklatex.com-cab8215853fccdd3a7b754dccd431986_l3.png "Rendered by QuickLaTeX.com")
(Note: if we define the Fourier Transform as 
Then the result could be a little different.)